Following my completion of the Self Driving Car specialization on Coursera, I wanted to take the learnings into something more practical. A limitation with using CARLA, which was the simulator used in the course, was the lack of realistic physics. The car behaved in strange ways when at the limit of tire grip. To address this, I turned to something familiar – racing games. Assetto Corsa was a game I had experience with and has a healthy modding community so it became my platform of choice for this project.
My goal for this project was to build a connection between the racing game and the back-end algorithm and use a basic “traditional” approach to generate an optimal target path for the car to follow. This would pave the way for future projects using more modern approaches such as deep learning or reinforcement learning. Below, I outline some of the key ideas behind the traditional approach and implementation details that makes the program drive successfully on the simulator. If you are not interested in the technical stuff but want to try out the program, feel free to jump to the last section.
Mathematical Optimization
The goal of path optimization is to minimize (or maximize) an objective function, which is similar to cost functions in supervised machine learning. The difference is that we don’t know the most optimal path so there are no actual values to compare against1. The most common approaches are to minimize the lap time directly and to minimize the curvature. However, we cannot compute the entire lap time or curvature in one go.
The traditional approach to path optimization divides a track into many discrete segments where each segment will have a value alpha between 0 and 1. Having a value 0 means the car is on the left-most part of the track and 1 represents the right-most part. This set of alpha values would then define the overall reference path. Typically, the initial guess for the reference path is 0.5. Now we can go ahead and compute the lap time or curvature.
Lap time can be calculated by dividing the length of each segment with the target velocity then summing up the results. The velocity profile computation is detailed in the next section. This approach is the most accurate (since minimizing lap time is the ultimate goal) but is computationally expensive. To address the speed issue, researchers have turned to minimizing curvature.
Curvature, typically denoted \( \kappa \), is the inverse of the instantaneous radius of a curve \( \kappa = 1 / r \). So minimizing the curvature is equivalent to maximizing the turning radius. Similar to lap time calculation, the objective function is the sum of curvatures at each segment. Minimizing curvature has been shown to yield similar lap times but is much faster to compute2. However, it’s not enough to know what path to follow. You also need to know how fast you should be following it.
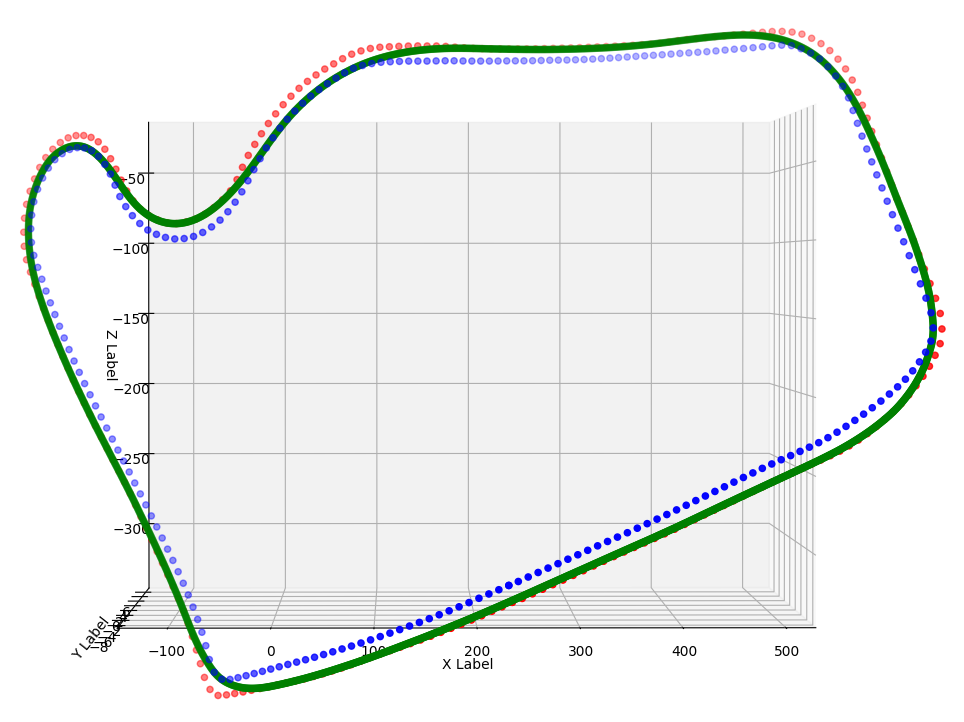
An optimized trajectory for the Red Bull Ring National track.
Velocity Profile
The velocity profile computation is divided into four steps. First, the maximum velocity is calculated for each segment. Second, you do a backward pass through the maximum velocities and compute the maximum deceleration. Third, you do a forward pass to compute the maximum acceleration while accounting for the maximum acceleration of the car at a given velocity. Lastly, to compute the final velocity profile, you take the minimum of the previous three steps.
Maximum velocity is a function of radius and maximum lateral acceleration \( v_{max}^{2} = a_{lat_{max}} \cdot r \). With a bigger turning radius, you can carry more speed through the turn. However, the formula doesn’t quite hold up when the track is not completely flat.
If you think about Nascar racing on oval tracks, the track surface is banked (where the side of the road that you are turning into is lower than the opposite side) which increases the maximum speed that can be carried through the turns. This is why many on/off ramps on highways will often have a slight banking.
Similarly, if the track is going uphill or downhill, then the car, impacted by gravity, would be rolling up/down the hill. This is an additional term in the car’s acceleration. I take both of these factors into account in my calculations but would be happy to chat about it if anyone is interested!
For the deceleration step, you start with a local minimum velocity and work backwards to calculate the highest speed you can slow down from. This is defined by \( v_{final} = \sqrt{2 \cdot a_{long} \cdot s + v_{init}^{2}} \) where \( s \) is the distance traveled and \(a_{long} = \sqrt{(\mu \cdot g)^2 - a_{lat}^{2}} \) with \( \mu \) the coefficient of friction of the tires and \( g \) the gravitational coefficient. In practice, a car is not able to maintain its maximum grip \( \mu \) due to load transfer which I briefly discuss in step 4 of this post. Therefore, some form of damping is required to account for the reduced grip. My code contains a rudimentary form of it which seems to work for the test track.
Acceleration follows similar steps to the deceleration step except you need to account for the force that the car can apply to its driven wheel. Even for race cars, this will not always be higher than the available grip. The formula for wheel force at a given velocity is defined by \[ F_{w} = \frac{ \tau \cdot e \cdot g_{i} * g_{f}} {r} \] where \( \tau \) is the engine torque in \(N \cdot m \)
\( e \) is the drivetrain efficiency
\( g_{i} \) is the gear ratio for gear \( i \)
\( g_{f} \) is the final drive ratio
\( r \) is the wheel radius in meters.
One thing I left out here was whether the car is front-wheel drive, rear-wheel drive, or all-wheel drive. Depending on the amount of vertical load on the driven wheels, the car’s overall coefficient of friction will be impacted. So the wheel force equation always overestimates the acceleration but not in a catastrophically detrimental way.
Clearly, there is much room for improvement in my implementation of the velocity profile calculation.It does not account for the load transfer during acceleration which limits the overall grip. In addition, it does not take into account aerodynamic forces that can play a major role in certain vehicles. However, it was good enough to get things working and as a solo developer, I had to manage my scope ruthlessly.
Controller
The algorithm used for the controller is largely from the first course of Coursera's self-driving car specialization. There were some tweaks made such as zeroing out the integral portion of the PID controller as I could not accurately model the velocity profile and the game will share the car’s exact velocity so there is no error that needs to be accounted for. The underlying algorithm largely remains unchanged.
To actually control the car in-game, I used the vgamepad package which is a virtual controller that runs on Python. Once the target throttle, brake, and steering values are calculated, the controller is updated with the target values. One thing to note is that I had to adjust control settings such as steering speed and steering gamma within Assetto Corsa to ensure that the controller inputs translated as close as possible to 1:1 in the game.
Results
How does this agent perform? A lap around the Red Bull Ring National track took around 1:06.8 with the agent. In comparison, the game’s default AI on 100% strength ran a best lap around 1:07.1. An elite human driver can likely go 1-2 seconds faster but I’m satisfied with the results.
Do you think you can beat my time? Download my code on GitHub and let me know how you get on!
How to get started
- Install Assetto Corsa (steam)
- Download AI Driver app for Assetto Corsa
- (optional) Download Content Manager
- Select car and track of choice from what's available
- Confirm tires are the default option
- Practice mode with ideal conditions
- (optional) If the track you want is not available, get AI Line Helper
- Use the “Track Left” button to map the left boundary
- Rename side_l.csv in the game installation directory to left.csv
- Use the “Track Left” button to map the right boundary
- Rename side_l.csv in the game installation directory to right.csv
- Copy into the content/tracks/track_name folder under the AC Self Driving repo below
- (optional) If the car you want is not available (YouTube instructions>
- Open Content Manager and go to the About section
- Click "Version" multiple times to enable developer mode
- Go to Content -> Cars and select the car you want
- Click "Unpack data" in the bottom row
- Copy into the content/cars/car_name folder under the AC Self Driving repo below
- Download the AC Self Driving repo
- pip install -r requirements.txt
- Run main.py
Code has been tested using Python 3.10 on a Windows 11 machine
1This paper describes a machine learning approach to solve the path optimization problem so there are certainly alternatives to the traditional path optimization approach.
2Kapania, N., Subosits, J., Gerdes, J. 2019. A Sequential Two-Step Algorithm for Fast Generation of Vehicle Racing Trajectories. https://arxiv.org/pdf/1902.00606.pdf, accessed January 30, 2023
